Exploring Parametric Curves: Finding the Area of an Inner Loop
Can you calculate the area enclosed by one of the inner loops formed by the curve $x(t) = 2 \cos(t) + \cos(5t)$ and $y(t) = 2 \sin(t) + \sin(5t)$?
1054 words 5 min Modified
Table of Contents
The Problem
From VOL. 55, NO. 22, MARCH 2024 edition of THE COLLEGE MATHEMATICS JOURNAL:
Consider the graph in the plane defined parametrically by
$$\begin{align*} x(t) = 2\cos(t) + \cos(5t) \\ y(t) = 2\sin(t) + \sin(5t). \end{align*}$$Find the area enclosed by one of the four inner loops.
— Greg Dresden, Washington and Lee University, Lexington, VA
Breaking Down the Problem
This problem revolves around a parametric curve, with equations for $x(t)$ and $y(t)$ that describe a looping, symmetric structure. The challenge is to calculate the area enclosed by one of the four inner loops. As soon as I saw the parametric nature of the problem, I realized I would need to use calculus, specifically integrals, to compute the area. The parametric area formula was the right tool for this task.
Parametric Equations for the Curve
The parametric equations for the curve are:
$$ \begin{align*} x(t) &= 2 \cos(t) + \cos(5t), \\ y(t) &= 2 \sin(t) + \sin(5t). \end{align*} $$
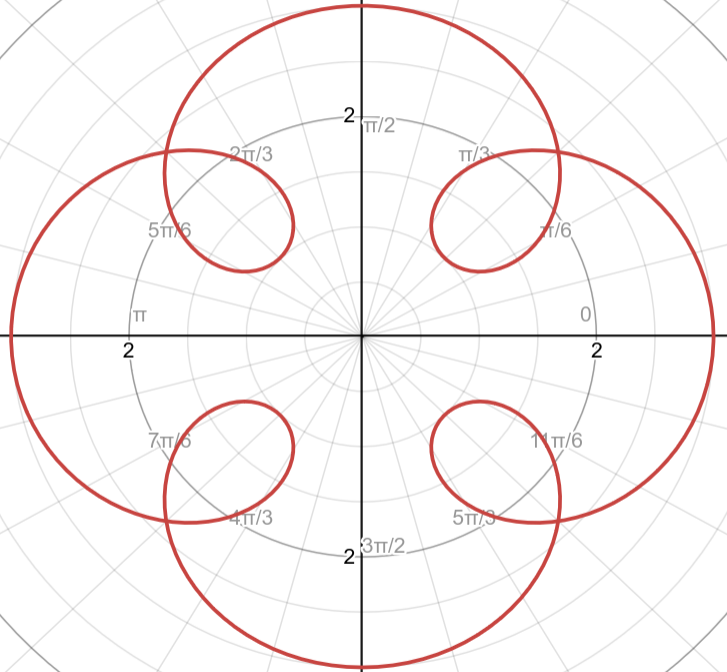
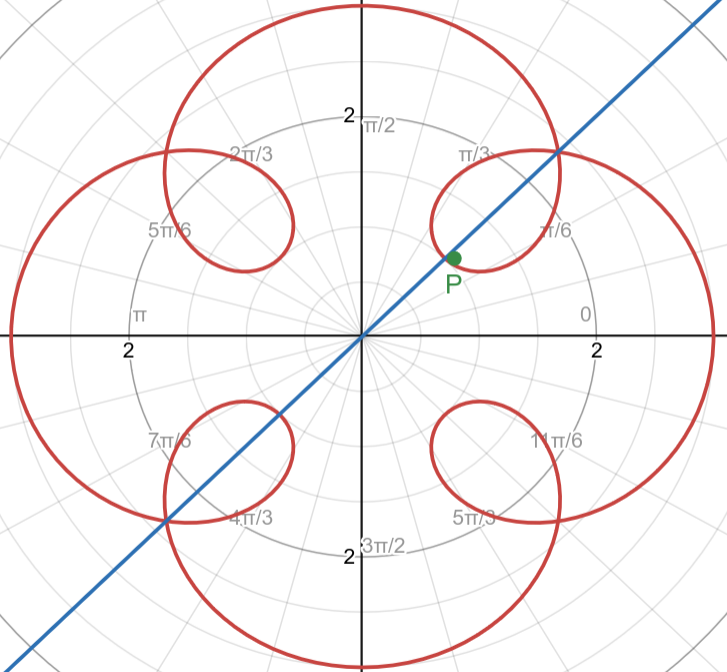
Notice that the point closest to the origin on the inner loop in the first quadrant is given by $x\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} = y\left(\frac{\pi}{4}\right)$, which lies on the line $y = x$. Let the point $P$ where the graph intersects itself in the first quadrant be given by $t = \alpha$ and $t = \beta$, where $0 < \alpha < \frac{\pi}{4} < \beta < \frac{\pi}{2}$.
From the symmetry of the curve, $\alpha$ and $\beta$ must be complementary, so that:
$$ \begin{align*} x(\beta) &= 2 \cos(\beta) + \cos(5\beta) \\ &= 2 \cos\left(\frac{\pi}{2} - \alpha\right) + \cos\left(5\left(\frac{\pi}{2} - \alpha\right)\right) \\ &= 2 \sin(\alpha) + \cos\left(\frac{\pi}{2} - 5\alpha\right) \\ &= 2 \sin(\alpha) + \sin(5\alpha) \\ &= y(\alpha) \end{align*} $$Since $x(\alpha) = x(\beta)$ and $y(\alpha) = y(\beta)$, then $P$ must lie on the line $y = x$. This is clearly true, as shown below:
Solving for $\alpha$ and $\beta$
Now, let’s examine the points of self-intersection we can apply the multiple-angle formulas to rewrite the parametric equations in terms of trigonometric identities:
$$ \cos(5t) = \cos t \left(1 - 12 \sin^2 t + 16 \sin^4 t \right), $$$$ \sin(5t) = \sin t \left(5 - 20 \sin^2 t + 16 \sin^4 t \right). $$
Thus, the parametric equations become:
$$ x(t) = 2 \cos(t) + \cos(5t) = \cos t \left(3 - 12 \sin^2 t + 16 \sin^4 t \right), $$$$ y(t) = 2 \sin(t) + \sin(5t) = \sin t \left(7 - 20 \sin^2 t + 16 \sin^4 t \right). $$
Where the curve intersects the line $y = x$, we have:
$$ \begin{align*} \sin t \left(7 - 20 \sin^2 t + 16 \sin^4 t \right) = \cos t \left(3 - 12 \sin^2 t + 16 \sin^4 t \right) \end{align*} $$Dividing both sides by $\cos t$, multiplying the right-hand side by $\frac{\sec^4{t}}{\sec^4{t}}$, and simplifying:
$$ \begin{align*} \frac{\sin{t}}{\cos{t}} &= \frac{3 - 12 \sin^2 t + 16 \sin^4 t }{7 - 20 \sin^2 t + 16 \sin^4 t} \cdot \frac{\sec^4{t}}{\sec^4{t}} \\ \tan{t} &= \frac{3(1+\tan^2{t})^2-12\tan^2t(1+\tan^2{t})+16\tan^4{t}}{7(1+\tan^2{t})^2 - 20\tan^2{t}(1+\tan^2{t})+16\tan^4{t}} \\ \tan t &= \frac{3 - 6 \tan^2 t + 7 \tan^4 t}{7 - 6 \tan^2 t + 3 \tan^4 t} \end{align*} $$To simplify further, let $u = \tan t$, leading to the following equation:
$$ u \left(7 - 6u^2 + 3u^4 \right) = 3 - 6u^2 + 7u^4. $$This expands to:
$$ 3u^5 - 7u^4 - 6u^3 + 6u^2 + 7u - 3 = 0, $$which factors as:
$$ (u - 1) \left(3u^4 - 4u^3 - 10u^2 - 4u + 3 \right) = 0. $$Given that $\tan{t} = u = 1$, we know $t = \frac{\pi}{4}$ is a solution, corresponding to the least upper bound before $\alpha$. The remaining real solutions for $t$ yield values for $\alpha$ and $\beta$, which can be determined by solving polynomial:
$$ 3u^4 - 4u^3 - 10u^2 - 4u + 3 = 0. $$Since $3u^4 - 4u^3 - 4u + 3$ is palindromic, we can divide by $u^2$ to get:
$$ \begin{align*} 3u^2 - 4u - 10 - \frac{1}{u} + \frac{3}{u^2} &= 0 \\ 3\left(u^2 + \frac{1}{u^2}\right)-4\left(u + \frac{1}{u}\right)-10 &= 0 \\ 3\left(\left(u+\frac{1}{u}\right)^2 - 2\right)-4\left(u + \frac{1}{u}\right)-10 &= 0 \\ 3\left(u+\frac{1}{u}\right)^2-4\left(u + \frac{1}{u}\right)-16 &= 0 \end{align*} $$Using the quadratic formula, we find
$$ u + \frac{1}{u} = \frac{2 \pm 2\sqrt{13}}{3}, $$and
$$ u^2 - \left(\frac{2(1 \pm \sqrt{13})}{3}\right)u+1=0. $$Since the discriminant $\Delta$ of this quadratic is $\frac{4}{9}(5 \pm 2\sqrt{13})$, and $5-2\sqrt{13} \lt 0$, the only real solutions are obtained for the positive case. Therefore:
$$ u = \frac{1 + \sqrt{13}\pm \sqrt{5+2\sqrt{13}}}{3} $$and the solutions for $\alpha$ and $\beta$ are:
$$ \alpha = \tan^{-1} \left( \frac{1 + \sqrt{13} - \sqrt{5 + 2 \sqrt{13}}}{3} \right), $$$$ \beta = \tan^{-1} \left( \frac{1 + \sqrt{13} + \sqrt{5 + 2 \sqrt{13}}}{3} \right). $$
For future reference, it’s important to notice that:
$$ \begin{align*} \beta - \alpha &= \tan^{-1}\left(\frac{2\sqrt{5+2\sqrt{13}}}{3 \cdot 2}\right) \\ &= \tan^{-1}\left(\frac{\sqrt{5}+2\sqrt{13}}{3}\right) \end{align*} $$and $\alpha + \beta = \frac{\pi}{2}$.
Finding the Area
To compute the area enclosed by one of the inner loops, we use the parametric area formula:
$$ A = \frac{1}{2} \oint_C x \, dy - y \, dx. $$Substituting the parametric expressions for $x(t)$ and $y(t)$ and simplifying:
$$ \begin{align*} A &= \frac{1}{2} \int_{\alpha}^{\beta} \left( (2 \cos t + \cos 5t)(2 \cos t + 5 \cos 5t) - (2 \sin t + \sin 5t)(-2 \sin t - 5 \sin 5t) \right) \ \mathrm{d}t \\ &= \frac{1}{2} \int_{\alpha}^{\beta} \left(4\cos^2{t}+12\cos{t}\cos{5t}+5\cos^2{5t}+4\sin^2{t}+12\sin{t}\sin{5t}+5\sin^2{5t}\right) \ \mathrm{d}t \\ &= \frac{1}{2} \int_{\alpha}^{\beta} \left( 9 + 12(\cos t \cos 5t + \sin t \sin 5t) \right) \ \mathrm{d}t \\ &= \int_{\alpha}^\beta\left(\frac{9}{2}+6\cos{4t}\right) \ \mathrm{d}t \\ \end{align*} $$Integrating, we get:
$$ \begin{align*} A &= \frac{9t}{2} + \frac{3}{2} \sin 4t \Big]_{\alpha}^{\beta} \\ &= \frac{9}{2}(\beta-\alpha)+3\sin{2(\beta-\alpha)\cos{2(\beta-\alpha)}} \\ \end{align*} $$Using the values of $\alpha$ and $\beta$, we find:
$$ \begin{align*} A &= \frac{9}{2} \tan^{-1} \left( \frac{\sqrt{5 + 2\sqrt{13}}}{3} \right) + 6 \sin(\beta - \alpha) \cos(\beta - \alpha) \cdot \cos\pi \\ &= \frac{9}{2}\tan^{-1} \left( \frac{\sqrt{5 + 2 \sqrt{13}}}{3} \right) - \frac{9 \sqrt{5 + 2\sqrt{13}}}{7 + \sqrt{13}} \end{align*} $$<EOF>
Therefore, the area of the region enclosed by one of the inner loops is:
$$ A = \frac{9}{2} \tan^{-1}\left(\frac{\sqrt{5 + 2 \sqrt{13}}}{3}\right) - \frac{9(\sqrt{5 + 2 \sqrt{13}})}{7 + \sqrt{13}} \approx 0.9108. $$This problem elegantly ties together parametric equations, trigonometric identities, and calculus. Through careful manipulation and integration, we arrived at a precise answer for the area (as well as a numerical approximation).